Smoke Control Using Pressurisation

Smoke control can be done through smoke extraction or pressurisation. Pressurisation is a method of preventing smoke from entering a space that is designated as an escape path or for fire-fighting purposes such as staircase or lift lobby by means of introducing fresh air from the external to create a positive pressure within the space. Pressure gradient ensures that smoke will always flow from region of high pressure to region of low pressure, away from the pressurised spaces.

Below is a calculator to help determine the total airflow required to pressurise a lift lobby and staircase, where both staircase and lift lobbies are pressurised at the same pressure level. The calculator is succeeded by a detailed guide on how each of the values from the calculator is computed, which helps us understand the concept so that we can apply to all other configurations, such as "staircase only" pressurised, or "lift lobbies only" pressurised.

The succeeding guide elaborates the method of computation of pressurisation of staircase and lift lobby that is commonly practiced in the industry based on BS 5588-4:1998, Fire Precautions in the design and construction of buildings – Part 4: Code of Practice for Smoke Control using Pressure Differentials or MS 1472:2017, Code of Practice for Fire Precautions in the Design of Buildings –Smoke Control in Protected Escape Routes using Pressurisation.

The steps are organized to help us better understand the concept of pressurisation based on the mentioned standards and how we determine the required airflow, hence our fan and duct/shaft size for pressurisation.

Please find after the calculator, the guide which explains the formulae from which we make up the calculator.

The calculator is supported by a paid third-party platform. It may take some time to load.

The guide below were being put together in a downloadable PDF version for your ease of reference. If you like us, download it by donating any amount in multiples of 10 dollars. Select quantity to vary donation amount to your closest desired amount.

Otherwise, you can always copy & paste the text should you need to work on the calculator with the guide be referred side-by-side. It is important to understand how the results are being derived from.

Regardless, this donation helps to keep our website running. We need your continuous support to grow and get better.

Note that we also add an option to purchase a premium excel version of our pressurisation calculator for the example shown below (without any locked Cells / Formula).

Step 1: Determine the Crack Length of Doors

Crack length is the sum of the “perimeter” around the door. It is calculated based on the types of doors using the formulae below.

Figure 1: Crack Length is the sum of lengths of all doors’ sides with gaps

Depending on the type of door (number of panels of the lift landing door), the same method is used to determine the crack length of a lift landing door.

Step 2: Determine the Leakage Area

By right the leakage area shall be the product of crack length and gap width of door. However, taking into consideration that all sides of doors may have different gap width, and the fact that different directions of swing of doors may affect leakages, the standards incorporates a factor to gauge the leakage area.

The standards dictate as shown in the table below the leakage area for the different doors of a typical size, taking more into consideration various factors which I believe include not only limited to crack length and gap width but also the direction of swing of door, function or mechanism, typical opening duration or etc, based upon the type of door.

The standard does not elaborate into details how we determine the leakage area of a door with crack lengths other than those mentioned in the table above. For a safer consideration, the standards suggest the “extrapolation” of the leakage area in the table in accordance to the crack length, as shown in the simple formula below.

For example, if the door is a non-standard double leaf door of height 2100mm and width 1850mm,

Actual Crack Length = 2w + 3h = 2(1.85) + 3(2.10) = 10 m

Adopted Leakage Area = 10/9.2 x 0.03 = 0.0326 m2

Step 3: Calculate the Air Leakage

The next crucial step is to determine the air leakages through the leakage area calculated from Step 2. The formula to look for is

These steps are repeated for each door and the total air leakages out of the pressurised space is the summation of air leakages across doors leading to non-pressurised spaces. Note that the pressure level is the difference in pressure between 2 spaces. If both lift lobby and staircase are pressurised at the same pressure level of 50 Pascal relative to the external, it is assumed that there is no air leakage across the door between the 2 spaces whose pressure differential equals to zero.

Step 4: Calculating the Resultant Leakage Area, Af into Lift Shaft through the Lift Landing Door

Air leakages through doors a normal staircase-external, staircase-accommodation, lobby-accommodation door, and lift landing door can be calculated as shown in steps 1 to 3. It is assumed that the leakage from the pressurised space to non-pressurised space is a parallel leakage path. However, the method of calculating the resultant leakage area into the lift shaft through the lift landing door, and then from the lift shaft to the external is resembling a combination of parallel and series leakage path.

Figure 2: Parallel leakage (Left) and series leakage path (Right)

Figure 3: Leakages into Lift Shaft. Resultant Leakages = Parallel leakages A//B in series with another parallel leakages C//D, A//B – C//D

That is an example of lift with through-opening configuration. Because there is countless combinations of lift configurations, it is important to understand the method to compute the resultant leakage path correctly in order to calculate leakages into each of the lift landing door.

The method that I use to sort things out is to define one lift shaft as one leakage path to study. Note that some lifts are not compartmented with brick walls but only by an ‘elevator divider beam’. In our study, the lift group separated only by a divider beam will be considered as 1 lift shaft only.

Figure 4: Lift Shaft 1 and Lift Shaft 2 of different configurations

Next, we sketch on a piece of paper the elevation view of each lift shaft with all its openings.

Figure 5: Sktech of Elevation of opening for Lift Shaft 1 (Left) and Lift Shaft 2 (Right)

“x2” denotes that there are 2 numbers of lift landing doors for the 2 lifts sharing the same shaft. Note that not all floors have the same configuration of lift landing doors. For example, for lift shaft 2, some of the floors have both lift having through-opening (level 1 to Level 3), some of the floors have one of the 2 lifts with through-opening (Level 4 and 5), some of the floors have both lift being single opening (Level 6). This is the reason we say that the combination of the lift opening configuration has no limitation.

After we mapped out the “opening schematic” of each of our lift shaft, we can now determine the resultant leakage area across the lift openings.

Figure 6: Parallel leakage path 1 (Red) is in series with Parallel leakage path 2 (Blue)

The formula that defines resultant leakage area for series and parallel leakage path are similar to the formula we use to calculate resultant Capacitance, or the opposite of what we use to calculate resultant Resistance of an electric circuit.

Combining the above 2 equations, with Parallel Leakage Area (Path 1) in series with Parallel Leakage Area (Path 2), the Resultant Leakage Area is combined into the equation below.

In other words, the Resultant Leakage Area can also be simply represented by

Figure 7: Parallel leakage path 1 (nAd) is in series with Parallel leakage path 2 (AF)

Referring to Figure 6, the specific Resultant Leakage Area for this example of configuration will be

Where Ad is the Leakage Area of 1 Lift Landing Door (as computed from Step 1 and 2) assuming all lift landing doors are of the same size, and Av is the Leakage Area, or essentially the area of the lift shaft vent.

Step 5: Calculating the Air Leakage through the Leakage Area computed from Step 4

Bear in mind that the Leakage Area of 1 Lift Landing Door, Ad is calculated using method in Step 1 and Step 2, similar to the other types of doors. Now with Ad and the Resultant Leakage Area (of the whole leakage path) through the lift shaft, Af, we are able to compute the Air Leakage (m3/s) across this path.

Effective Air Leakage across 1 lift landing door is represented by the equation below. It is basically the air leakage through the resultant leakage area (of the whole leakage path) divided by the number of lift landing doors.

Note that Ad is only the leakage area of one lift landing door to a non-pressurised space, regardless of the actual leakage path through the lift shaft’s configuration. Taking into consideration the configuration of the lift shaft openings, the effective leakage area into each of the identical lift landing doors shall be taken as Af/n.

Also note that n should be the number of lift landing doors for one of the parallel leakage paths only. This is because the same amount of airflow, Qeff passes through the entire leakage path once only, as shown in the Figure 8 below. In this case, n is taken from the path involving the pressurised side (Leakage path 1, into the lift shaft). Since the parallel leakage path of the pressurised space (Leakage Path 1) is of our interest, and all the openings in this parallel leakage path is identical, the total airflow through the whole leakage path (resultant leakage area) shall suitably be divided by number of openings in this path only. With this, we can determine the air leakage from the pressurised space into each (1) lift landing door, Qd.

Note that Qd is the air leakage through one of the lift landing doors only. This is clarified to avoid the confusion that may arise as to why the air leakage reduces when the number of lift landing doors, n increases. When n increases, it is logical that the air leakage through each of the lift landing door reduces. But certainly, the overall leakage, Qeff shall increase with n. The air leakage also very much depends on the area of the second parallel leakage path (Leakage 2, out of Lift Shaft). If any of the series leakage path area is small, the overall effective leakage area (resultant leakage area, Af will be suppressed by the “bottleneck”.

This is the same concept as, when two resistors are connected in parallel, the resultant resistance is very low if any one of the resistors has very low resistance, no matter how large the other resistances are. As mentioned, “parallel” in electrical resistance is analogous to “series” in airflow. If any of the leakage paths in series with the other leakage paths has small leakage area, the resultant leakage area will be small, no matter how big the other areas are.

If any of the capacitors connected in series with the other capacitors has low value of capacitance, the resultant capacitance will be low, no matter how high the other capacitances are.

Figure 8: Parallel leakage into lift shaft is equal to leakage out of the lift shaft

It is also good that we browse through some of the important parameters stated by the standard. Factor F is the ratio of the resultant leakage area to the leakage area of one lift landing door.

Substituting Af=FAd, Qd can also be represented by

Step 6: Calculating the Total Air Leakage from each Lift Lobby

The total Air Supply flowrate, QL required to overcome the leakages through all the openings from a lift lobby is calculated by summing up as shown below, air leakages through all Lift Landing Doors – which can be from different shafts – and all doors leading to a less pressurised or non-pressurised space. Also as specified in the standard, we multiply the sum of air leakages with a safety factor of 25% to account for all other unidentified leakages such as those from the voids of walls.

Using the same method, QS for staircase pressurisation can be computed, except that we can skip the computation for QF through lift shafts. Also, instead of calculating for individual Lift Lobby whose configuration may be different from one another, the leakage air calculation for staircase involves only 1 stairwell as a whole.

Case Studies

To help understand what we have been discussing so far, let’s make use of the following example to show how QL is calculated.

Figure 9: Lift-lobby and staircase typical layout for case study

Note that this is the total air leakage for one lift lobby only. To size the overall Lift-lobby Pressurisation Shaft and Fan, this total leakage has to be multiplied with the number of Floors or number of Lift Lobbies intended to be pressurised. If the Lift Lobbies from each level differs in configuration from one another, we either work out level-by-level and obtain their sum, or take the lift lobby with the highest computed value of QL multiplying it with the number of floors.

This is the overall air flowrate required to pressurise the entire stairwell at 50 Pascal. Because both Staircase and the Lift Lobbies are also pressurised at the same pressure level, the pressure differential across the staircase-lobby door is equal to 0. Therefore, there is no significant leakages into all staircase-lobby doors. However, at ground level, the staircase has an exit to the external, non-pressurised space whose leakage must be accounted for.

The leakage airflow calculation is case-specific. In this example, the computed flowrate Qs is only able to overcome leakages across the single door leading to the external at ground level. Please be reminded that for other cases where there are other doors connecting to non-pressurised space such as those at every floor’s staircase landing, this value has to be multiplied with the total number with such doors connecting to non-pressurised spaces.

Step 7: Calculating the “Top Up” Air Required based on different scenario:

Both Staircase and Lift-Lobbies are Pressurised (Example Cont’d)

The airflow introduced to pressurise the Staircase and Lift Lobby – QS and QL, respectively – is only able to overcome leakages across the doors in closed condition. Imagine that if you are introducing only 0.158m3/s of air to the entire stairwell, the pressure will be lost easily when the staircase-external door is being opened for escape during a fire outbreak. Pressure takes a long time to build-up in the deep stairwell with such a low rate of fresh air intake, hence will not be able to afford anymore intermittent opening and closing of doors.

The same case applies to the Lift Lobby.

Things get a little more complicated when we want to determine if the calculated airflow is still able to achieve our intended pressure level when the doors are being opened for escape purposes in the event of fire. Fortunately, the standards have specified the minimum conditions and assumptions to make as guidelines for our design. It is important that we understand the general concept to be able to apply it to various cases.

To make things short, according to the standards, a “Top Up” air to the value of QS or QL calculated from step 5 is needed to maintain the pressure level for intermittent opening of doors, if the original computed values do not meet specified requirements. One of the main requirements is to maintain at least 1 m/s egress velocity of air across all opened doors.

For better understanding, we will be using this example shown in Figure 10 for our detailed explanation. This is a configuration of a 6-floor pressurised staircase and lift lobby with 1 lift shaft of 1 lift car.

Figure 10: Example of Lift Lobby and Staircase that are both pressurised, with all doors closed

Now, let us understand the different types of airflow stated by the standards when different doors are open. We are required to fulfill the requirement of 1 m/s air velocity across those open doors for at least 2 scenarios in our design, namely

2-door open (The Lobby-Accommodation Door is open & The Staircase-Lobby Door is open)
1-door open (The Lobby-Accommodation Door is open & The Staircase-Lobby Door is closed)

2-door open (The Lobby-Accommodation Door Open & The Staircase-Lobby Door Open)

For buildings within 20 stories of height, take any one floor and assume that both staircase-lobby door and lobby-accommodation door are open, then imagine the airflow that will occur as a result of that.

Remember that QL and QS are the calculated values of airflow that we need to introduce to each lift lobby and the stairwell, respectively, to overcome leakages over closed doors to non-pressurised spaces. Referring to Figure 11, observe that now the lobby-staircase door and lobby-accommodation door for Level 3 are both open. With QL and QS sized just enough to overcome leakages, we can speculate that the most of the air from QL at Level 3 as well as the stairwell, QS, have already gushed through the 2 open doors as indicated in the yellow arrows below, rendering both Lift Lobby L3 and the entire stairwell’s pressure to drop to – most probably – a state that is equalised with the external accommodation (differential pressure ≈ 0 Pa), depending on the duration of which the door is being held open.

Figure 11: 2-Door open. Both Lobby-Staircase Door and Lobby-Accommodation Door are open

The space highlighted in yellow in Figure 12 (a) below is the space that encounters pressure loss due to opening of doors. This is the space affected by the opening of doors that requires our attention.

Figure 12 (a): Highlighted space showing the space that loses pressure as a result of the 2-door open scenario

Despite the pressure loss for the region, a few types of airflow from other lift lobbies whose doors are closed will flow into the this “low-pressure zone” to “assist” in maintaining the air pressure level, or in which case as specified in the standards, to “assist” in achieving the minimum 1 m/s egress velocity of air across the opened doors.

As shown in Figure 12 (b), the pressure-gradient forces a decent amount of airflow from all other lift lobbies whose doors are closed (except Level 3), to leak through the closed lift landing doors’ gaps, into and along the lift shaft, and then into the lift lobby whose doors are open (Level 3). This is marked with the blue arrows below, and we name this air flow as QA.

Figure 12 (b): QA is the leakage of air from other lift lobbies whose doors are closed to the lift lobby that loses pressure via the lift shaft

From Figure 13, apart from QA, another significant amount of airflow also originates from all other lift lobbies whose doors are closed (except Level 3), leaking through the closed lobby-staircase doors’ gaps into and along the stairwell. Eventually, this airflow travels down the pressure-gradient into the lift lobby whose doors are open (Level 3). This is marked with the green arrows below, which we name as QT.

Figure 13: QT is the leakage of air from other lift lobbies whose doors are closed into the stairwell and lift lobby that loses pressure

After we have understood the different types of airflows under the 2-door open scenario, the egress velocity of the sum of airflow into the affected space can be estimated by dividing the airflow sum with the total area of opened doors. This will be shown later in our calculation example.

We have learnt how to calculate the values of QS and QL from Step 5. From the standards, the values of QA and QT are represented by the equations given below.

However, the above equations can sometimes be confusing, because they are being simplified to an extent that they can only be applied if all the lift shafts have the same configurations. Often, this will not be the case. As shown in our example from Step 4, some lifts share a common shaft separated only with divider or separator beams. On the other hand, most of the fire lifts has its dedicated RC compartmentation. This renders each of the lift shafts with unique configurations of openings.

In order to be able to modify the equation to suit our specific configuration, we need to first understand how the equation came about.

Let’s have a look at the equations below, which explains how the above equations from the standards are being derived from. These less-simplified equations may look more complicated but are mostly applicable to all combinations of configurations of lift shafts.

Determining QA

The complete equation to determine the value of QA shall be as shown below, which may be applicable to various cases and examples. The equation looks a bit complicated but let’s explain in detail what each of those parameters means.

Figure 14: Example showing QA, m, n, QS and QL

From previous definitions, we have understood that QA is the air that leaks from lift lobbies whose doors are closed, through the closed lift landing doors of the respective floor, and then travel along the lift shaft before leaking out through the closed lift landing door to the lift lobby whose doors are open. QA1 as shown in the flow in Figure 14 above, represents QA specifically for Lift Shaft 1. QA2, on the other hand, represents QA specifically for lift shaft 2. Note that both Lift Shaft 1 and 2 have totally different configurations.

For Lift Shaft 1, the value of m1 is equal to 1. There is only 1 lift landing door to a lift lobby for Lift Shaft 1. For Lift Shaft 2, the value of m2 is equal to 2. There are 2 lift landing doors to a lift lobby for Lift Shaft 2.

When all doors are closed, for Lift Shaft 1, the value of n1 is equal to 6. There are 6 lift landing doors opening into pressurized space. For Lift Shaft 2, the value of n2 is equal to 12. There are 12 lift landing doors opening into pressurized space. However, after the doors on Level 3 is open, lift lobby 3 loses pressure and becomes an unpressurised space. Therefore, n1 is reduced to 5 and n2 becomes 10.

Af is the resultant or effective leakage area across a specific lift shaft – Af1 for Lift Shaft 1, Af2 for Lift Shaft 2. If you have already forgotten what they are, please refer to the previous explanation in Step 5. You can also refer to our previous case study where we computed Af1 and Af2 case-specifically. However, due to the changes in the m and n values, Af1 and Af2 needs to be re-calculated when considering the doors open. This will be shown in the example after we determine how the equation is derived.

Subscripted n resembles the nth number of lift shaft – if there are more than 2 lift shafts, the count shall continue until the nth shaft with parameters such as QAn, Afn, mn and nn.

n represents the number of lift lobbies that is pressurised. n’ is the total number of floors or lift lobbies.

AD is the leakage area of the closed lobby-staircase door for a lift lobby. Al1 is the sum of other leakage areas of the lift lobby to non-pressurised spaces, excluding the Lift Landing door or the lobby-staircase door that has already been accounted for.

Last but not least, n is the total number of lift lobbies. Different from n1 and n2, the value of n shall be irrespective of any lift shafts’ number of openings. n-1 represents the number of lift lobbies that is pressurised, deducting the 1 lift lobby that loses pressure.

Now that we know all parameters to calculate QA, it will not be hard for us to determine how the formula is derived from.

The formula equates a ratio of airflow with the ratio of leakage area that corresponds to the airflow.

In essense, the ratio of air leakage into a lift shaft from all lift lobbies to the overall air flow in all lift lobbies, is equal to the ratio of the area of leakage into the lift shaft from one lift lobby to the overall parallel leakage area for one lift lobby. Note that the lobby whose doors are opened is assumed to have lost pressured air and therefore to be deducted from the sum of pressurised air QL x n.

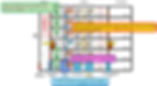
Figure 15: Example showing the Sum of pressurised air for all Lift Lobbies (Green), Leakage Area into a Lift Shaft per Lift Lobby (Purple), Sum of Air Leakage into Lift Shaft for All Lift Lobbies (Orange), & Total Leakage Area per Lift Lobby (Blue)

Before we substitute all our parameters into the equation above, there is one more thing to take note of – there is one general assumption being made as stated by the standards in the computation of QA, that “the Airflow out of each lift shaft past the closed lift entrance door, is taken as 1/3 of the total airflow into the lift shaft.”

For the 2-door open scenario for 1 lift lobby, the air leakage out of a lift shaft is assumed to be 1/3 of that flow into it. For more than 20 stories of lift lobbies, where the standard requires that we assume 2-door open for 2 lift lobbies, this “1/3” should be replaced with “1/4”.

Figure 16: Example showing the relationship between airflow leaking into and out of a lift shaft

This means that:

QA = 1/3*Sum of all pressurised air that leaks into a lift shaft

Therefore, Sum of all pressurised air that leaks into a lift shaft = 3 QA

Substitute this into the equation,

With this, when we substitute all other parameters for Lift Shaft 1, the equation becomes

This explains the equation that we previously thought was very complicated.

If we study the example that we have here, the equation can be substituted further with:

Figure 17: Example showing QL(n-1) (Green), Af/n (Purple), 3QA (Orange), & AD + Al1 + Af1/n1 + Af2/n2 (Blue)

Quick Recap

At this point, you may be wondering how we get leakage area into a lift shaft per lift lobby to be Af/n. For this, you may want to recap the formula below from Step 5.

At the beginning of Step 5, it has been explained that Ad is only the leakage area of one lift landing door to a non-pressurised space, regardless of the actual leakage path through the lift shaft’s configuration. Taking into consideration the configuration of the lift shaft openings, the effective leakage area into each of the identical lift landing doors shall be taken as Af/n.

For this example or for most of the cases – except those where a same lift shaft has different number of lift landing doors opening on each lift lobby, e.g. 2 openings on Level 2, 3 openings on Level 3, no opening on Level 4 etc. – the denominator “5” here can be replaced with n, because m/n (2/10, 3/15, 4/20) will always give a value of 1/n – where n is the number of pressurised lift lobbies.

Therefore, assuming all lift lobbies have the same lift opening configuration (which is often the case), the following equation can be applied, where the subscripted n from Afn represents the nth number of lift shaft opening, which may be confused with n, i.e. as aforementioned, the number of lift lobbies that is pressurised.

In the rare occasion where each lift lobby has a unique lift landing door configuration for a specific shaft, the value of QA can be computed for each of the lift lobbies’ “2-door” open, and the least value of QA shall be adopted. In other words, we shall take the lift lobby with the lowest QA summed from all shafts to be the lift lobby with the 2-door open.

Although each lift shaft tends to have the same configuration of lift landing opening for all lift lobbies, we often come across different opening configurations among different lift shafts. Therefore, we need to also compute airflow QA for the other lift shafts, such as Lift Shaft 2, 3 and so on, if any. The total QA should be taken as the sum for QA for each of the lift shafts.

Figure 18: More often than not each lift shaft has the same configuration of opening for all levels of pressurised lift lobbies, & different configurations between one and other lift shafts

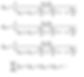
As we have emphasised, this is the method we use if any of the lift shafts are of different opening configurations from the other. If they happen to be the same, each of the equations can then be further simplified to resemble those stated in the standards.

Back to our example, to obtain the value for QA

The leakage areas from our previous calculations Al1 and AD can be adopted from the previous calculations. However, the value of the effective or resultant leakage area, Af for each of the lift shafts has changed following the changes in the number of lift shaft’s openings into pressurised and non-pressurised spaces in the event of the opening of doors causing the involved lift lobby(s) to lose pressure.

The standards set a guideline for the estimation of the value of Af, in the form of Factor F = Af/Ad, as shown in the Table below. However, this estimation is only valid when a few assumptions are made, including that there shall be only 1 vent opening of the shaft into unpressurised space, and the vent area shall be less than or equal to 0.1 sq. meter.

Only when these conditions are fulfilled, when 1 floor of lift lobby’s door(s) is open (1 lift lobby loses pressure), factor F can be referred from column 3; and when 2 floors of lift lobby’s door(s) are open, factor F can be referred from column 4.

For all cases other than that, it will be compulsory to know how to calculate the value of Af versatilely like we previously do. In our case, the vent is not the only opening to non-pressurised spaces because we have through-openings for certain floors in the lift shaft.

Therefore, let’s re-determine the new value of Af1 and Af2 for our lift shafts when 1 floor of lift lobbies losses pressure, in order for us to calculate QA and QT.

Figure 19: New Sktech of Elevation of opening for Lift Shaft 1 (Left) and Lift Shaft 2 (Right) considering Lift Lobby 3 as a Non-pressurised space

Because of the 2-door open at lift lobby 3, lift lobby 3 now loses pressure. Meaning to say, lift landing door opening into lift lobby 3 becomes an opening into an unpressurised space. Af shall be re-calculated as follows.

Determining QT

To determine QT, the same concept and the same formula as QA is used.

As mentioned, this formula equates a ratio of airflow with a ratio of leakage area that corresponds to the airflow.

In essence, the ratio of air leakage into the stairwell from all lift lobbies to the overall air flow in all lift lobbies, is equal to the ratio of the area of leakage into the stairwell from one lift lobby to the overall parallel leakage area for one lift lobby. Note that the lobby whose doors are opened is assumed to have lost pressured air and therefore to be deducted from the sum of pressurised air QL x n.

In order that we can understand faster, we disclosed the formula before we try to understand how QA is being derived from. Now, using the same concept, let’s try to derive the formula for QT.

Figure 20: Example showing QL(n’-1) (Green), AD (Purple), QT (Orange), & AD + Al1 + Af1/n1 + Af2/n2 (Blue)

Unlike air leakage through closed lift landing door where the air leakage out of the lift shaft is assumed to be one third of that entering the lift shaft, it is assumed that 100% of air leaking through closed staircase-lobby doors will pass through the open door. Therefore, sum of pressurised air that leaks into the stairwell through closed staircase-lobby doors for all lift lobbies is equal to QT. Note that the subscripted n represents the nth number of lift shaft opening, and n’ being the total number of lift lobbies.

Again, assuming all lift lobbies have the same lift opening configuration for all levels, the following equation can be applied, where n represents the number of pressurised lift lobbies, and n’ represents the total number of lift lobbies (n = n’ – 1). Note that the standards are using only 1 parameter n to represent the number of lift lobbies, because it assumes all lift lobbies are pressurised, and changes in the value of Factor F takes into consideration the effective leakage area for lobbies that loses pressure due to opening of doors as reflected in Table of Factor F.

As we emphasised again, this is the formula we use if any of the lift shafts are of different opening configurations from one another. If all lift shafts happen to be identical, the equation can be simplified further to resemble that stated in the standards.

Back to our example, to obtain the value for QT,

With all the air flow involved, we can now calculate the egress velocity across the 2 open doors. From the standards, the “passing score” for the egress velocity of a door is 1 m/s. This is the minimum velocity that we expect to prevent smoke infiltration from the opposite direction of airflow. If this 1 m/s egress velocity cannot be achieved, we most probably have to “top up” our staircase/lobby pressurisation air, QS and QL.

Figure 21 (a): Airflows QS & QT into the highlighted space enclosed by, and then egress through the staircase-lobby door

Egress velocity across the lobby-staircase door that is open – circled red in Figure 21 (a) – is determined by taking the total airflow across the door, which is essentially the total airflow into the highlighted space in Figure 21 (a) (the space enclosed by the lobby-staircase door) divided by area of the open door. You can either take the area of the lobby-staircase door to be 2.1 x 0.93 = 1.953 m2, or just assume it as 1.6 m2 as specified in the standards. This value also applies to a double-leaf door, of which only one of the 2 leaves of doors is considered open.

Note that the total air flow into the space, in this case QS + QT, is multiplied with a factor of 0.6 to account for the leakage air flow resistance. Although the egress velocity across the lobby-staircase door is found to be less than 1 m/s, the standards allow us to “pass” provided the other door, the lobby-accommodation door as the first cut-off from smoke/fire, manage to achieve the minimum 1 m/s egress velocity.

Figure 21 (b): Airflows QS, QT, QL & QA into the highlighted space enclosed by, and then egress through the lobby-accommodation door

Now, the total airflow into the highlighted space enclosed by the lobby-accommodation door is the sum of QT, QS, QL and QA. All of these airflows is assumed to flow into the space and then down the pressure-gradient across the lobby-accommodation door to the external, unpressurised space, with velocity across the lobby-accommodation door being:

Since the egress velocity of this lobby-accommodation door exceeds 1 m/s, we do not need to top up any air to our pressurisation air QS and QL, which on their own, is deemed able to contribute to the egress velocity that minimises smoke entry and maintain pressure with intermitent opening and closing of doors.

After the 2-door open scenario is studied, the pressurisation air for the staircase and lift lobby shall remain as our previous calculation of QL = 1.458 m3/s and QS = 0.158 m3/s, without the need of adding any “top up” air to achieve 1 m/s egress velocity.

1-door open (The Lobby-Accommodation Door is open & The Staircase-Lobby Door is closed)

In addition to the 2-door open scenario that we have studied previously, according to the standards, we also have to calculate the egress velocity of air across the lobby-accommodation door, under the 1-door open scenario. The concept will be the same as for 2-door open, including the requirement to assume 2 floors of the set of door(s) open when the number of floors, n exceeds 20. This will be shown in another example later on.

Figure 22: Airflows QL, QA, and Leakage QAD into the highlighted space enclosed by, and then egress through the lobby-accommodation door

To calculate the egress velocity across the opened lobby-accommodation door, the total airflow into the highlighted space of interest (space that loses pressure) is determined, corrected and then divided by the area of opened door, i.e. 1.6 sq. meter.

We know that the leakage area of the lobby-staircase door AD, and the leakage across it is negligible under all-doors-closed condition, whereby both the staircase and lift lobbies are pressurised at the same pressure level. However, when the lobby-accommodation door is open, it is assumed that the involved lift lobby’s pressure is equalised with the accommodation, therefore the air leakage becomes through AD becomes significant

Now the egress velocity for the lobby-accommodation door can be determined as follows. Note that QS and QT now becomes only an air leakage QAD into the lift lobby.

After the 1-door and 2-door open scenarios have both been studied, the final pressurisation air for the staircase and lift lobby shall remain as our previous calculation at QL = 1.458 m3/s and QS = 0.158 m3/s, without the need of adding any “top up” air to achieve 1 m/s egress velocity across open doors, for “1-door” and “2-door open” condition.

Note that QL is the pressurisation air for each lift lobby. If all the lift lobbies are sharing a common lift-lobby pressurisation system, the fan and shaft shall be sized at 3100 cfm x 6 lift lobbies = 18,600 cfm.

Only Lift Lobbies are Pressurised (Staircase is Natural Ventilated)

In most of the cases, the staircase is tucked to the building parameters. If a staircase fulfills the minimum opening area required to be deemed as natural ventilated, no pressurisation to the stairwell is required.

If we work on our previous example with the staircase now not pressurised, slight changes to the value of QL should be made, as the leakage across the lobby-staircase door becomes significant.

The new value of lift lobby pressurisation airflow, QL, is as follows:

2-door open (Lobby-Staircase Door Open & Lobby-Accommodation Door Open)

Figure 23: Airflows QL & QA into the highlighted space enclosed by, and then egress through both lobby-accommodation & staircase-lobby doors

When the staircase is natural ventilated, it is assumed as being equalised with the external that all air gashes into the stairwell are lost to the external. Not only would we not get any “assistance” from QT through the lobby-staircase door, the opening of the lobby-staircase door introduces a new egress area for the air inside the lift lobby. The new egress velocities for the doors now become:

For both staircase-lobby door and lobby-accommodation door, the egress velocity is obtained by dividing area of both doors to unpressurised spaces.

1-door open (Lobby-Staircase Door Closed & Lobby-Accommodation Door Open)

Figure 24: Airflows QL & QA into the highlighted space enclosed by, and then egress through the lobby-accommodation door

With QL = 1.538 m3/s, the egress velocity of 1 m/s can still be achieved under the 1-door open scenario, but fails under the 2-door open scenario, when the staircase now considered an “external”, unpressurised space. Each door is only achieving 0.598 m/s of egress velocity. In other words, a top up air to the amount sufficient for both doors to have a minimum 1 m/s egress velocity under the 2-door open scenario is necessary.

The total airflow required to achieve the minimum egress velocity will be as shown below, working back the above formula by substituting 1 m/s as the egress velocity.

Now, with the addition of the top up airflow, Q Top up, the total airflow into lift lobby, i.e. the sum of QS, QT, QL, QA, and Q Top up – in which case QS and QT does not exist – is able to achieve 1 m/s egress velocity at both the lobby-accommodation and staircase-lobby doors.

Figure 25: Airflows QL, QA & Q Top Up into the highlighted space enclosed by, and then egress through the lobby-accommodation door

Usually, if the staircase is also pressurised, it is best that the top up air is usually added to the Staircase airflow, QS, in order that it can assist both the staircase-lobby and lobby-accommodation doors to achieve the 1 m/s egress velocity required.

Therefore, using the same example but only with the lift lobby being pressurised while staircase natural ventilated, after the 1-door and 2-door open scenarios have both been studied, the final pressurisation air for the staircase and lift lobby from our previous calculation of QL = 1.538 m3/s, requires a Top up airflow in order to achieve 1 m/s egress velocity during the 2-door open scenario.

Note that Q Top Up is only added once to the entire pressurisation system serving all the 6 lift lobbies, Q LPS after it is summed up from individual pressurisation air for each lift lobby, QL. The airflow into each lift lobby after the Top up airflow is added becomes 1.895 m3/s per lift lobby, QL’.

The original QL is the minimum airflow sufficient to overcome leakage when all doors are closed, whereas the Top Up air is the additional airflow required for the purpose of achieving 1 m/s egress velocity during occasions when doors are being opened.

Determining the Area of Pressure Relief Damper (PRD)

Whenever a Top Up air is introduced to a staircase or lift lobby, a pressure relief damper (PRD) is often required to regulate pressure so that pressure will not build up too high (>60 Pascal) when doors are kept closed for long period of time. It is recommended that the damper is motorised and be controlled by a feedback from a pressure differential sensor within the pressurisation duct.

The size of the pressure relief damper is determined based on the amount of Top Up Air.

Since the Top Up air is added to all floors of lift lobbies, this PRD area can either be added to the main pressurisation duct serving all 6 lift lobbies, or to individual lift lobbies with each of the area divided by 6, i.e. 0.37/6 = 0.062 m2 per lift lobby.

This is the minimum area of PRD required based solely on the amount of top up air. This PRD area shall be increased further if it is found that the pressure differential across the pressurised space exceeds the 60 Pascal limit even after considering the area of PRD.

For instance, the pressure differential between a pressurised lift lobby and the external can be calculated using the fundamental formula below:

Previously, we calculated the Airflow QL based on the area of leakages and differential pressure level. Now we are only doing the exact reverse – to get back the differential pressure across the space using our airflow QL and Area of leakages.

Working backwards

exactly by assuming all doors’ closed, without the additional 25% for unidentifiable leakages, prior to the addition of Top up air and without the PRD, we shall obtain back the value of 50 Pascal:

2. by adding to the conditions in (1), the Top Up airflow and the corresponding area of PRD that we sized based on it, the calculated pressure differential shall still be the same:

3. (1) and (2) above are computed for our understanding purposes only. The actual calculated pressure differential of the pressurised lift lobby to the external shall be complete with the addition of Top Up air and the PRD sized based on it, together with the 25% addition (no longer divide 1.538 by 1.25) for unidentifiable leakages in the original QL determination:

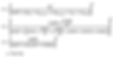
From (3), we know that the area of the PRD that we sized based on top up air, 0.062 m2 per lift lobby, may not be sufficient to relieve our pressure to 50 Pascal. Therefore, we shall substitute “0.062” from the above equation with an unknown: APRD, and P with a value of 50 Pascal, before solving for APRD.

With the initial Area of PRD revised to 0.1134 m2 per lift lobby, or 0.68 m2 in total (for 6 lift lobbies), the pressure can be better regulated at 50 Pascal. However, as mentioned, the PRD would be able to have better control if it is motorised thereby able to reduce in area or close up completely when the pressure drops below tolerance levels.

Calculating the Pressure Differential across a Lobby-Accommodation Door

More often – with the exception that the staircase is not pressurised – the failure to achieve 1 m/s egress velocity occurs during the 1-door open scenario, across the lobby-accommodation door. This is because when the staircase-lobby door is closed, QS and QT are limited, and becomes only a leakage, QAD into the involved lift lobby.

With the condition that the egress velocity across the lobby-accommodation door being able to achieve 1 m/s under the 2-door open scenario, even if the lobby-accommodation door could not achieve the egress velocity under the 1-door open scenario, we do not need the Top Up air, provided the pressure differential across the staircase-lobby door exceeds 45 Pascal.

Pressure differential across staircase-lobby door is computed using the equation that we have just used, but with modified, case-specific parameters.

Figure 26: Pressure Differential across the Lobby-Staircase Door exceeding 45 Pa removes the necessity of adding a Top Up air under the 1-door open scenario

From the above computation, if the lobby-accommodation door could not achieve the 1 m/s egress velocity under the 1-door open scenario, we will need to add the top up air accordingly, because 33.5 Pascal is below the 5 Pascal tolerance (from design pressure level of 50 Pascal) as mentioned by the standards.

On the other hand, with pressure level, P above 50 Pascal, the area of the PRD can be estimated using the method we have used just now, by working backward the equation to get A from P and Q.

High-rise building (Assume Door Opening on 2 Floors)

2-door open for 2 floors (Lobby-Staircase Doors & Lobby-Accommodation Doors Open)

If the number of pressurised lift lobbies exceeds 20, or n>20, it is stated in the standards that we need to assume 2 doors of 2 floors to be open, and all open doors shall still achieve the minimum 1 m/s egress velocity.

With 2 lift lobbies’ 2 doors open, slight modification to the formulae of QA and QT should be made. As mentioned, the “1/3” factor shall be replaced with “1/4” and “n-1” shall be replaced with “n-2”, indicating that we deduct 2 numbers of pressurised lift lobbies. “n1” or the number of lift landing doors into pressurised space for each lift shafts shall also be deducting the number of lift landing doors in the 2 floors of lift lobbies that loses pressure. This may sound complicated, so let’s work this out on our example.

Figure 27: Example showing 2 floors with 2-door open scenario that applies to buildings where total number of lift lobbies, n > 20

The formula to determine QA is as follows. Note the changes as mentioned above from the QA that we used in our last example with 6-storey lift lobbies.

Now, we have 22 floors of lift lobbies of the same configuration. Assuming there is still only 1 staircase-external door leading to non-pressurised space at the ground level, QS = 0.158 m3/s shall remain unchanged. However, as the number of pressurised floors increases, the effective air leakage into each lift shaft changes, QL = 1.458 m3/s calculated for each of the lift lobbies shall be re-calculated.

Figure 28 (a): Sketch of elevation showing the number of lift landing door openings into pressurised space and non-pressurised space for each lift shaft when all doors are closed

As mentioned, the leakage areas from our previous calculations Al1 and AD can also be adopted from the previous calculations. However, the value of the effective or resultant leakage area for each of the lift shafts needs to be revised following the significant change of the number of lift lobbies, n.

Figure 28 (b): Sketch of elevation showing the number of lift landing door openings into pressurised space and non-pressurised space for each lift shaft during 2-door open for 2 floors

From the illustration in Figure 28 above, n1 (number of lift landing door from lift shaft 1 opening into pressurised space) is taken as 20, while n2 (from lift shaft 2) is 40, both excluded openings into lift lobbies that have lost pressure. From Figure 28, it is shown that the total pressurised space and non pressurised space for lift shaft 1 is 20 and 2 respectively, whereas for lift shaft 2, 40 and 44 respectively.

Again, as mentioned, if the configuration of lift landing doors for all levels for a lift shaft is the same (i.e. the lift shaft has the same configuration of lift landing door opening into all pressurised floors), the above equations can be simplified to the equation below, with the only change comparing to the QA equation for 1 floor’s 2-door open scenario being the factor, “1/3” to “1/4”.

Regardless, for our better visualisation of how the formula is being simplified or derived, we will still be using both equations to work out this example.

Similar to QA, for QT, the total pressurised air QL reduces by one lift lobby from “QL(n-1)” to “QL(n-2)”:

Now, as shown in Figure 29, the egress velocity across the staircase-lobby door shall be the corrected total airflow into the highlighted space, divided by area of 2 open doors from 2 different floors.

Egress velocity for the open staircase-lobby door,

Egress velocity for the open lobby-accommodation doors,

Figure 29 (Left): Example showing the egress velocities across the 2 sets of lobby-staircase doors being the total airflows into the highlighted space, QS + QT divided by door areas

Figure 29 (Right): Example showing the egress velocities across the 2 sets of lobby-accommodation doors being the total airflows into the highlighted space, QS + QT + 2QL + QA divided by door areas

Bear in mind that both QT and QA are not coming out of nowhere. They leak from other floors of pressurised lift lobbies, as represented by the green and blue arrows, respectively, into the highlighted space which loses pressure.

The pressurisation air for the staircase and lift lobby may remain as QL = 1.458 m3/s and QS = 0.158 m3/s, without the need of adding any “top up” air to achieve the minimum 1 m/s egress velocity under this “2 floors’ 2-door open” scenario. Note that 2 lift lobbies will involve 2 QL to be considered in the flow to the highlighted space.

Optionally, some engineers prefer their design to be safer in the sense that they can also achieve 1 m/s egress velocity with an extra door open, i.e. the staircase-external door at the staircase’s ground level. In that case, the egress velocity can be calculated by dividing by total area of the 3 doors, 4.8 sq meter.

Figure 30: Optional 3-door open scenario for egress velocity computation

1-door open for 2 floors (Lobby-Staircase Doors Closed & Lobby-Accommodation Doors Open)

Now, let’s calculate the egress velocity across the open lobby-accommodation doors for 2 floors of lift lobbies under 1-door open scenario. As shown in Figure 31, the egress velocity across the 2 lobby-accommodation doors (in total 3.2 sq meter) now involves airflow QA, 2 QL for 2 lift lobbies, and leakage across 2 staircase-lobby doors, 2 QAD. It is good to notice that the minimum egress velocity is harder to achieve under the 1-door open scnario than the 2-door open scenario, because QT becomes only leakages, QAD into the lift lobbies.

Figure 31: Airflows 2QL, Sum of QA, and Leakage Air 2QAD into the highlighted space enclosed by, and then egress through the open lobby-accommodation door

Egress velocity for the open lobby-accommodation doors, based on illustration in Figure 32,

Figure 32: Example showing the egress velocities across the 2 sets of lobby-accommodation doors being the total airflows into the highlighted space, 2 QAD + 2QL + QA divided by door areas

Note that QAD is the leakage across the closed staircase-lobby doors between the staircase pressurised at 50 Pascal relative to the lift lobbies that loses pressure.

After the 1-door and 2-door open scenarios have both been studied, the final pressurisation air for the staircase and lift lobby shall remain as per our previous calculation at QL = 1.458 m3/s and QS = 0.158 m3/s, without the need of adding any “top up” air to achieve 1 m/s egress velocity across open doors, under 1-door and 2-door open condition.

Note that QL is the pressurisation air for each lift lobby only. If all the lift lobbies are sharing a common lift lobby pressurisation system, the fan and shaft shall be rightfully sized at 2610 cfm x 22 lift lobbies = 57,500 cfm.

Reference

Department of Standards Malaysia. (2017). MS 1472:2017 Code of Practice for Fire Precautions in the Design of Buildings – Smoke Control in Protected Escape Routes using Pressurization. Shah Alam.

British Standards Institution. (1998). BS 5588-4:1998 Fire Precautions in the design and construction of buildings – Part 4: Code of Practice for Smoke Control using Pressure Differentials. United Kingdom.